最近刷到接雨水，学习到可以用单调栈这种巧妙的数据结构，所以在此整理总结。

简介

首先栈（Stack）是一种线性表数据结构，是一种只允许在表的一端进行插入和删除操作的线性表，实现了 LIFO。

而单调栈（Monotonic Stack）是一种特殊的栈，在栈的基础上做了限制，要求从栈顶到栈底的元素必须是单调递增/递减的。

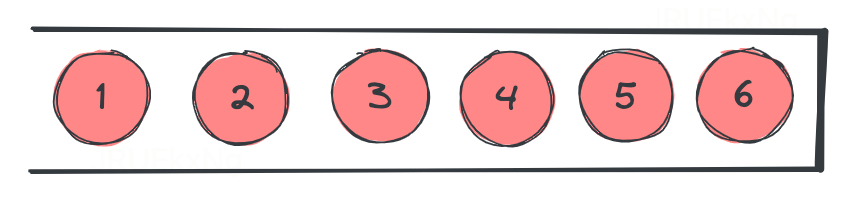
• 单调递增栈：栈顶到栈底单调递增。只允许比栈顶元素小的元素入栈，否则需要把比当前元素小的元素全部弹出，再入栈（保证了栈中元素大于当前准备入栈的元素，实现单调递增）。

  

• 单调递减栈：栈顶到栈底单调递减。只允许比栈顶大的元素入栈，否则需要把大于当前元素的栈中元素全部弹出，再入栈（保证栈中元素总小于当前元素，实现单调递减）。

  

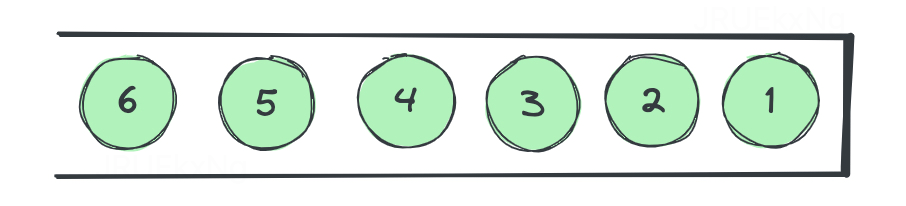
有些文章定义的顺序是从栈底到栈顶，这不重要，本文以栈顶到栈底为准描述单调栈。

例题

739. 每日温度

leetcode 739
给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

解：

暴力想法就是对于每天的温度遍历整个数组找到下一个更高的温度，求下标差值，时间复杂度 O(n2)。而使用单调栈能够实现 O(n)，思路就是利用单调递增栈，维护遍历过的温度，对于当前遍历到的元素，对比其和栈顶元素的大小。

• 若大于栈顶元素，说明出现了比栈顶温度大的温度，同时直接入栈也破坏了单调递增性，于是弹出栈顶元素，记录其与当前元素的坐标差值。继续比较新栈顶元素。
• 若小于或等于栈顶元素，说明没有出现比栈顶大的温度，直接入栈，此时也满足单调递增。

遍历完成后剩下在栈中的元素说明找不到下一个更高的温度，则其差值为0。

本题单调栈中保存的是数组下标方便求下标差值，单调栈题目经常存的是数组下标。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
                // 题目有前提数组至少包含1个元素，所以不需要判空
        int[] ans = new int[temperatures.length];
        Stack<Integer> stack = new Stack<>(); // save index
        stack.push(0);
        for (int i = 1; i < temperatures.length; i++) {
                        // 当前元素大于栈顶的情况
            while (!stack.isEmpty() && temperatures[stack.peek()] < temperatures[i]) {
                int topIndex = stack.pop();
                ans[topIndex] = i - topIndex;
            }
                        // 这里是空栈或当前元素小于等于栈顶的情况
            stack.push(i);
        }
        return ans;
    }
}

42. 接雨水

leetcode 42
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

解：

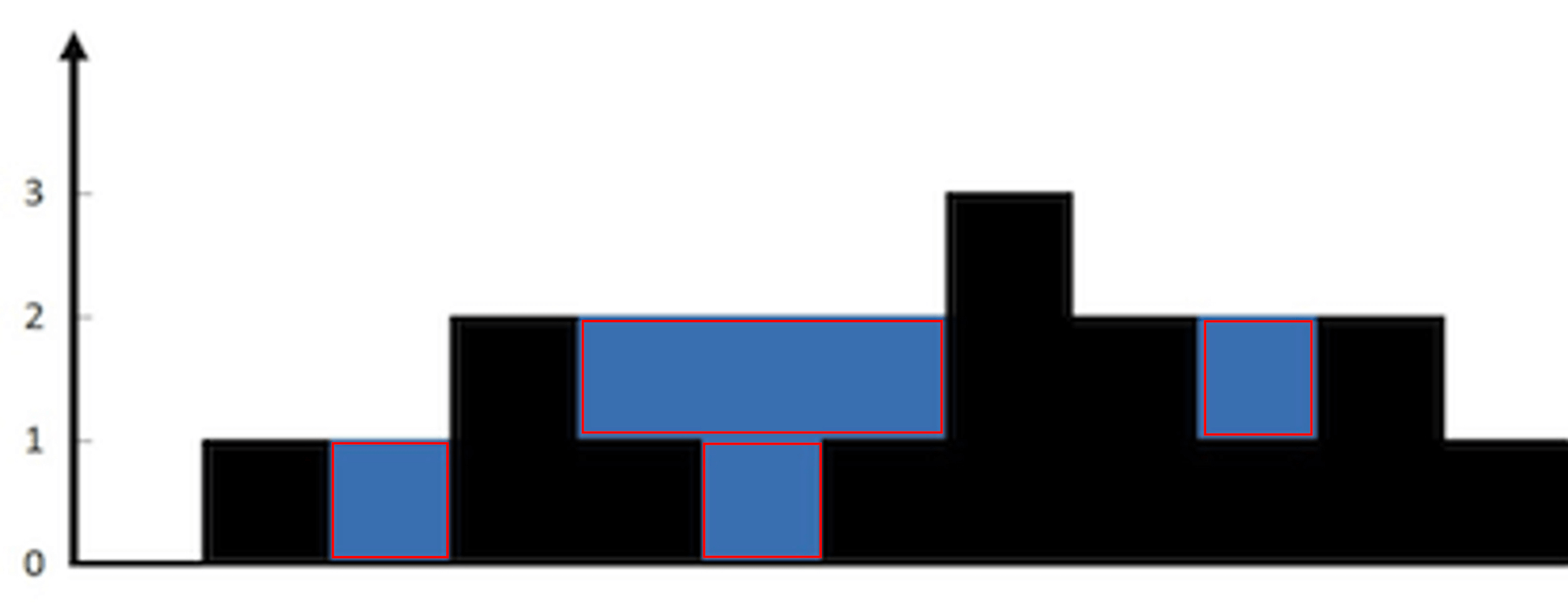
暴力解法是按列求每列左边最高柱子和右边最高柱子的，根据其中较低者求雨水面积后求和，时间复杂度O(n2)；而采用单调栈的方式可以优化到O(n)，单调栈解法是按行求面积。具体思路是采用单调递增栈，目的是找到以当前遍历到的柱子高度为底（或是之前遍历过的柱子为底，此时底长度需要求和），分别找到其左边和右边较高的柱子形成凹槽，求得凹槽面积。过程是遍历每个柱子：

• 若当前遍历到的柱高度小于栈顶高度，说明还无法积累雨水，所以当前高度入栈，这也是为什么是单调递增栈。
• 若遍历的柱子高度和栈顶相等，可以直接入栈或是栈顶出栈再把当前高度入栈，二者的结果是一样的，直接入栈需要计算面积（此时和栈顶高度差为0，所以面积为0，具体可以看下一步计算面积的逻辑），而出栈再入栈只需要计算最后入栈的高度面积，所以我们可以选择出栈再入栈避免重复计算。
• 若当前遍历到的柱高度大于栈顶高度，此时一定形成凹槽了（可能没有凹槽的场景：1. 此时栈里面的高度有可能全部相等；2. 栈里只有一个高度，没法组成左柱。场景 1 相等情况我们由上一步已经排除了，场景 2 需要我们做判断排除并出栈（因为已经是无效的高度了），所以这里的「一定」已排除这两种场景），凹槽以栈顶元素为底部，此时计算凹槽面积：右柱 = 当前遍历高度，左柱 = 下一个栈顶高度，得凹槽高度 = Min(左柱高度，右柱高度) – 当前底高度，底长度 = 右柱下标 – 左柱下标 – 1。计算完成后弹出栈顶，若下一个栈顶仍然小于当前遍历的高度，循环当前步骤。

单调栈的解法不同于暴力解法按列求面积，而是按行求面积。

class Solution {
    public int trap(int[] height) {
        int sumAns = 0;
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        for (int i = 1; i < height.length; i++) {
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                int botIndex = stack.pop();
                if (stack.isEmpty()) {
                    break;
                }
                int leftHeightIndex = stack.peek();
                int heightReal = Math.min(height[i], height[leftHeightIndex]) - height[botIndex];
                int bot = i - leftHeightIndex - 1;
                sumAns += (bot * heightReal);
            }
            if (stack.isEmpty()) {
                stack.push(i);
            } else if (height[i] == height[stack.peek()]) {
                stack.pop();
                stack.push(i);
            } else {
                stack.push(i);
            }
        }
        return sumAns;
    }
}

84. 柱状图中最大的矩形

leetcode 84)
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

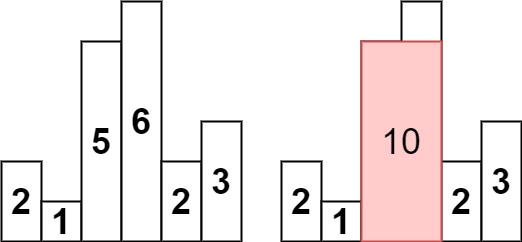
解：

暴力的想法是对每个柱子向左向右求出第一个比它小的柱子，得到最大的长宽求面积，最后比较得到最大面积，需要 O(n2)。单调栈思路：对于每个柱子而言，只要下一个柱子比它高，它的面积就可以增加。于是我们维护一个单调递减栈保存遍历过的柱子，直到遍历到比栈顶小的柱子，此时需要把栈顶弹出，计算以栈顶为高度，而宽度是以当前遍历到的柱子为右边，以下一个栈顶为左边柱的坐标差减 1。若新的栈顶仍然大于当前遍历到的元素，则再次执行计算面积逻辑。直到不满足该条件，继续往后遍历。

本题单调栈还有一个细节，需要在原数组首尾补 0：

• 首部补 0 的原因是：例如数组是 [1, 2]，此时遍历到 2 ，由于总共才 2 个高度，需要计算面积时没有左柱，无法计算结果；
• 而尾部补 0 的原因是，例如 [1, 2, 3] 这样的递增数组，到最后都无法找到比栈顶小的柱子，无法满足条件触发计算。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] heights2 = new int[heights.length + 2];
        heights2[0] = 0;
        for (int i = 0; i < heights.length; i++) {
            heights2[i+1] = heights[i];
        }
        heights2[heights.length + 1] = 0;
        int max = 0;
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        stack.push(1);

        for (int i = 2; i< heights2.length; i++) {
            while (!stack.isEmpty() && heights2[i] < heights2[stack.peek()]) {
                int topIndex = stack.pop();
                int weith = i - stack.peek() - 1;
                int height = heights2[topIndex];
                max = Math.max(max, weith*height);
            }
            stack.push(i);
        }
        return max;
    }
}

85. 最大矩形

leetcode 85
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

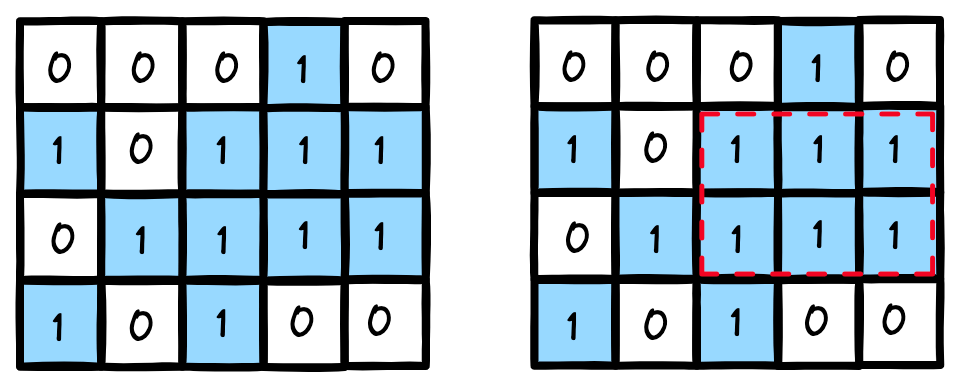
解：

暴力想法是每个点作为矩形左上角坐标，向右下扩散并验证是否构成矩形，然后求最大面积，时间复杂度太高 O(n2m2)（设矩形为 n 行 m 列）。在暴力的基础上，可以进行优化，对于每个点先进行预处理，统计所在列截止所在行连续 1 的个数。此时计算最大矩形我们需要对于每行的每个非 0 点，进行向左向右遍历，统计大于等于当前数字的点个数（构成矩形的条件是遍历到的点的数字需要大于等于当前点数字），另外对于（当前数字 * m）小于等于目前最大面积的点可以直接剪枝不计算，矩形面积等于当前点数字与统计的点个数之积，时间复杂度 O(nm2)。

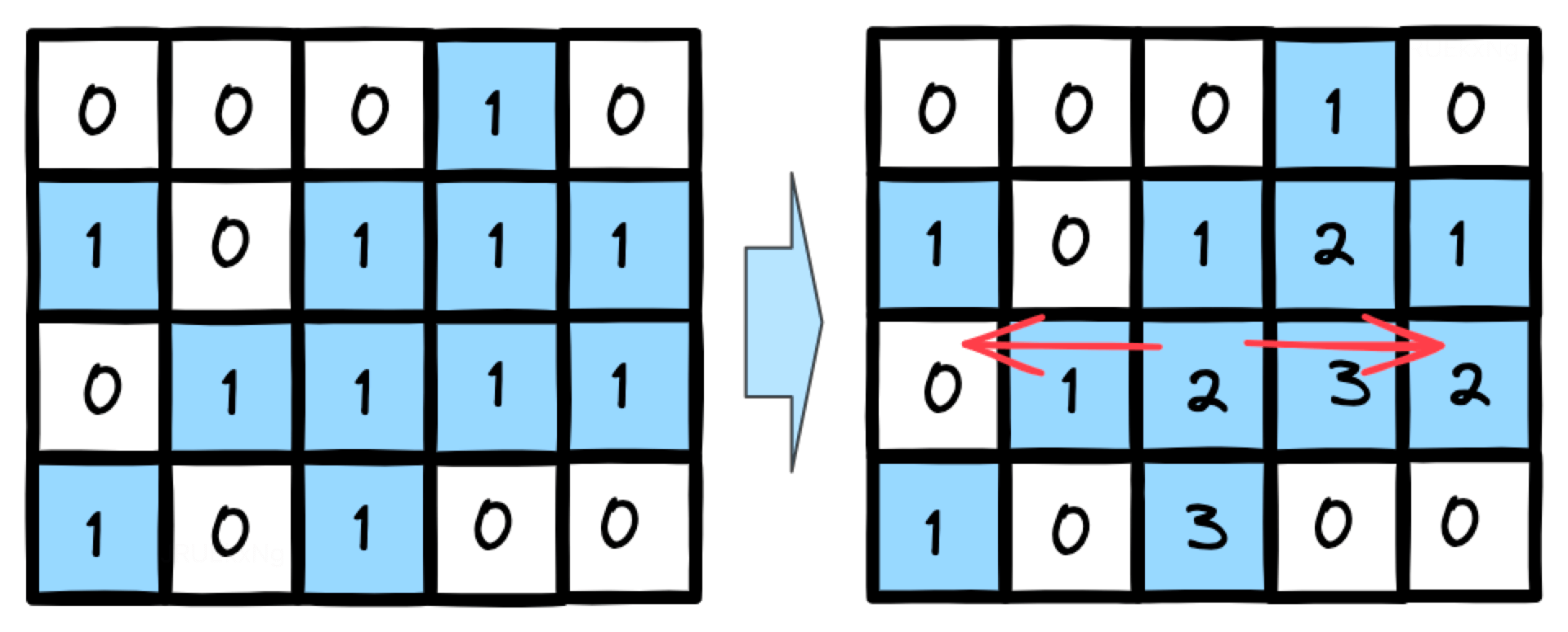
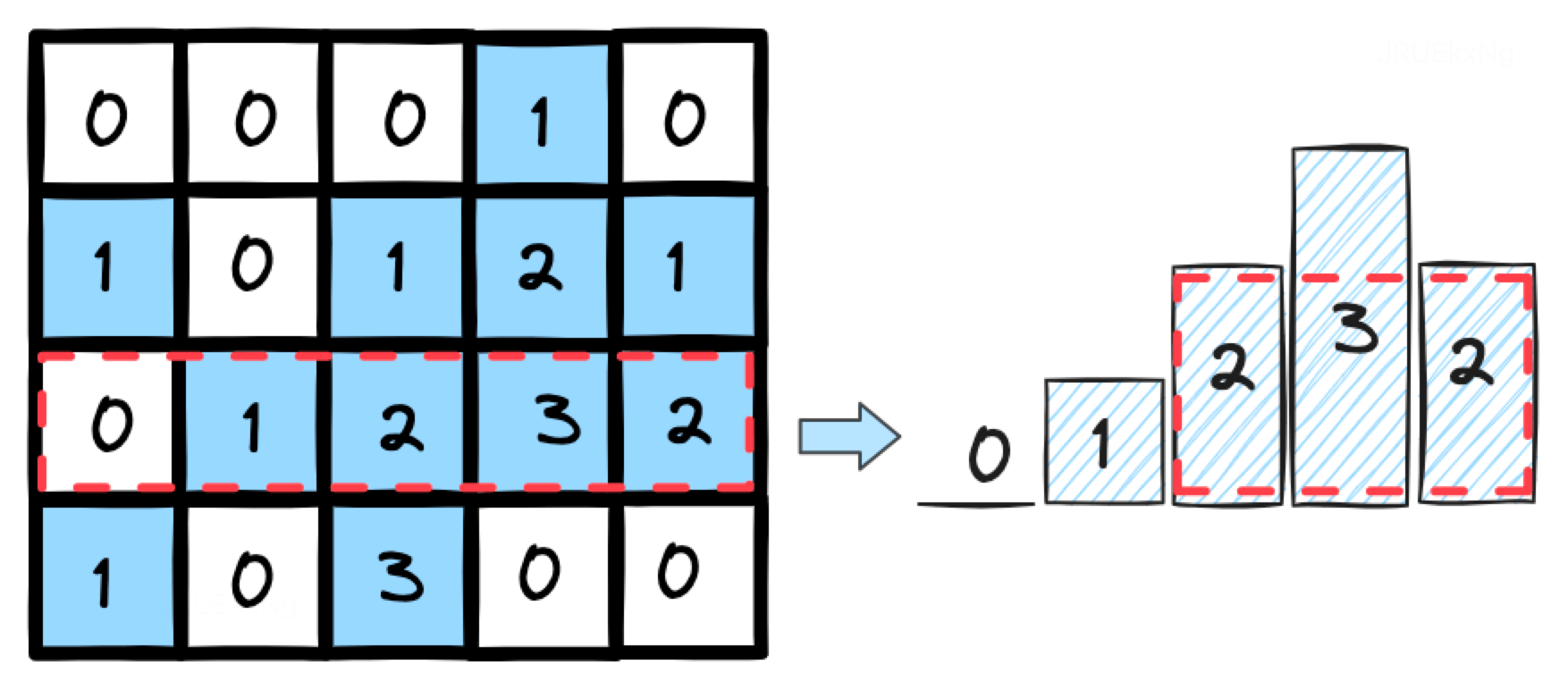
我们还可以把本题转化为 84 题柱状图最大矩形利用单调栈求解，具体过程：从优化暴力解法我们可以得到每行统计连续列为 1 个数的矩阵，对于该矩阵每行可以转化为右边的柱状图，构成的矩形高度就是当前点的数字，最大矩阵面积的构成逻辑和优化暴力的想法一样，但是计算过程从柱状图可以明显看出可以转为84题的单调栈思路，复用计算面积函数，时间复杂度 O(nm)。

class Solution {
    int max = 0;
    public int maximalRectangle(char[][] matrix) {
        int[][] heights = new int[matrix.length][matrix[0].length];
        // n 行 m 列
        for (int n = 0; n < matrix.length; n++) {
            for (int m = 0; m < matrix[0].length; m++) {
                if ('1' == matrix[n][m]) {
                    if (n == 0) {
                        heights[n][m] = 1;
                    } else {
                        if ('1' == matrix[n - 1][m]) {
                            heights[n][m] = 1 + heights[n - 1][m];
                        } else {
                            heights[n][m] = 1;
                        }
                    }
                }
            }
        }
        for (int n = 0; n < heights.length; n ++) {
            largestRectangleArea(heights[n]);
        }
        return max;
    }

    private int largestRectangleArea(int[] heights) {
        int[] heights2 = new int[heights.length + 2];
        heights2[0] = 0;
        for (int i = 0; i < heights.length; i++) {
            heights2[i + 1] = heights[i];
        }
        heights2[heights.length + 1] = 0;
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        stack.push(1);

        for (int i = 2; i < heights2.length; i++) {
            while (!stack.isEmpty() && heights2[i] < heights2[stack.peek()]) {
                int topIndex = stack.pop();
                int weith = i - stack.peek() - 1;
                int height = heights2[topIndex];
                max = Math.max(max, weith * height);
            }
            stack.push(i);
        }
        return max;
    }
}

总结

单调栈主要用于解决寻找下/上一个较大/较小的元素问题。